一覧
当塾について
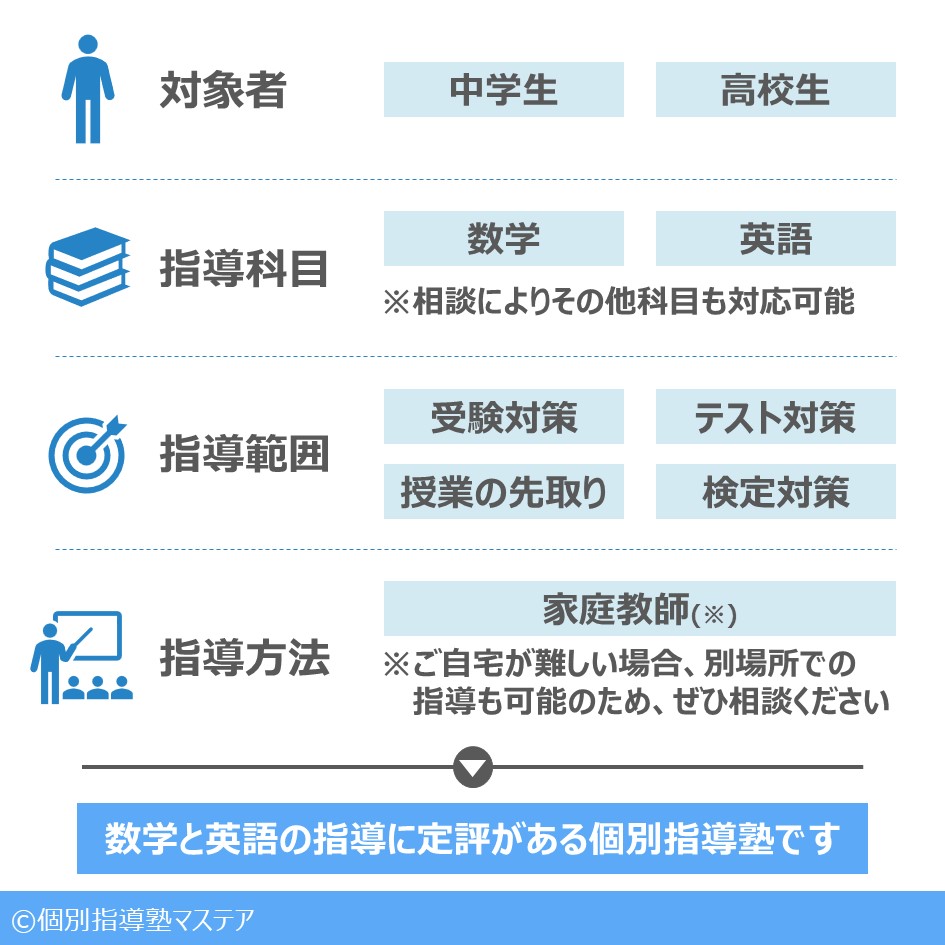

数学と英語の指導に力を入れている学習塾です。
その実績は次でまとめています。
※その他科目についても指導が可能な場合がありますのでぜひご相談ください。
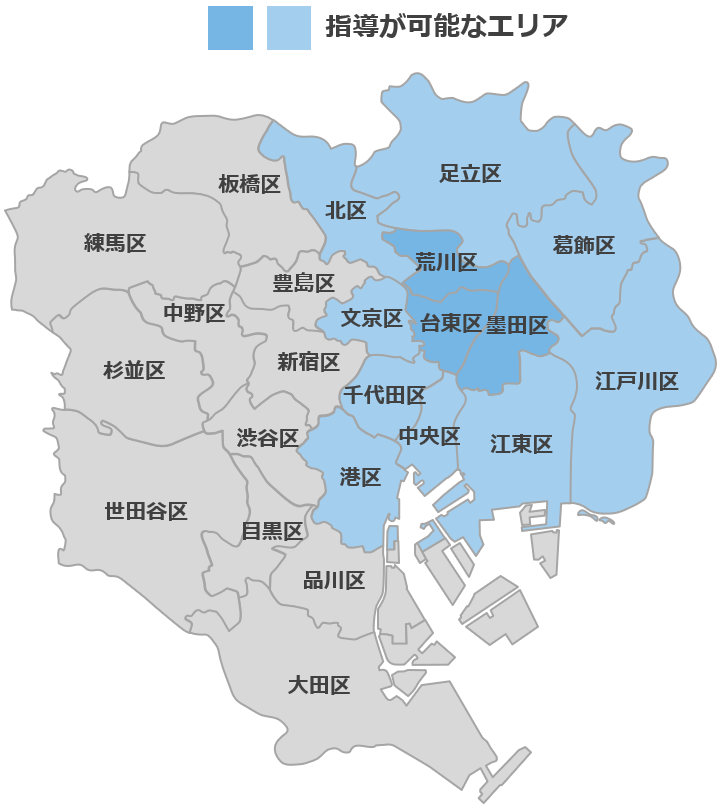
青色の区が指導可能エリアとなります。

具体的には 墨田区、台東区、荒川区、葛飾区、江戸川区、江東区、中央区、千代田区、港区、文京区、北区、足立区 の12区が指導可能エリアになります。
- 高校3年生の時に全国模試で数学全国1位を取得
- 指導者として6年で200人超え
- 数検準1級
- FP1級技能士
- 大手金融機関にて数学・統計の専門家として勤務後、外資コンサルにて一定の成果を残し今に至る

指導者の一面とFPの一面の両方を兼ね備えています。
当塾の実績
| 年度 | 学校名 | 人数 |
| 2022 | 早稲田大学 | 1名 |
| 明治大学 | 1名 | |
| 東海大学 | 1名 | |
| 2021 | 上智大学 | 1名 |
| 立教大学 | 1名 | |
| 青山学院大学 | 1名 | |
| 明治大学 | 1名 | |
| 東京理科大学 | 1名 | |
| 芝浦工業大学付属高校 | 1名 |

小さい塾ですが、 有名な大学も含め 実績は徐々に出てきています。
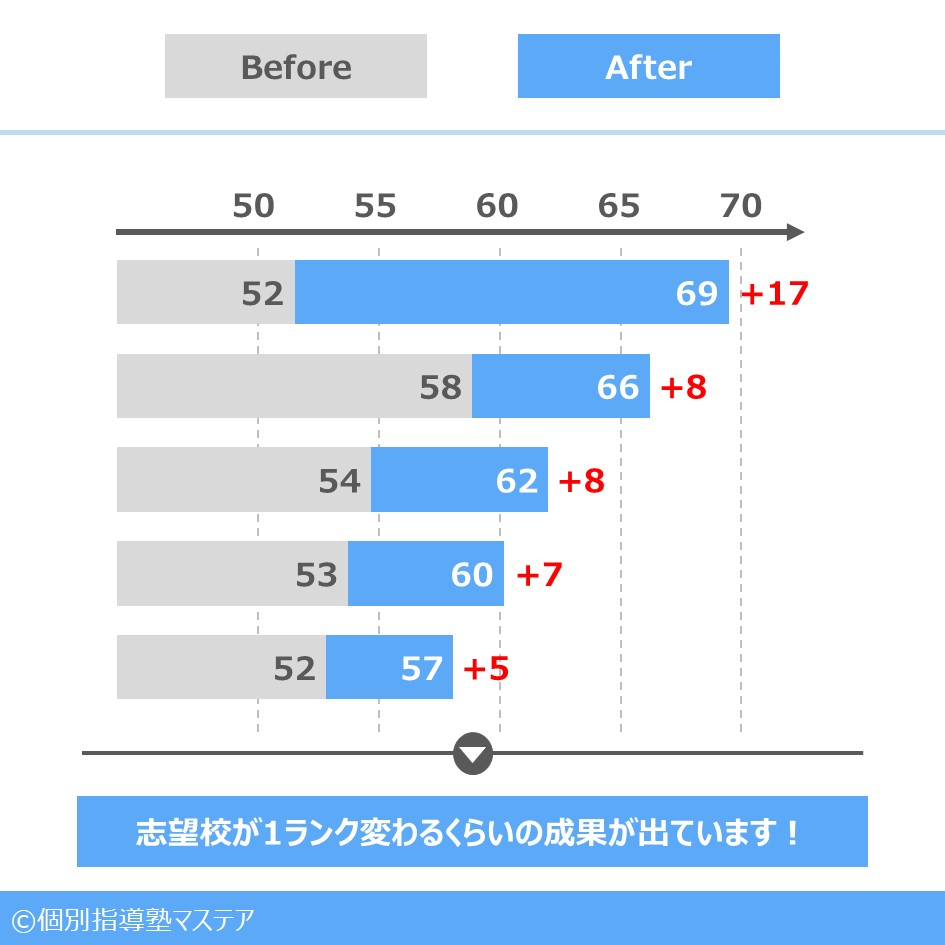

成果を全てお見せすることはできませんが、 指導には学力向上に一定の効果がある と自負しています。
なぜ実績が出せるのか?

当塾が目に見える実績が出る理由は、以下2つのことを徹底しているためです。
- 目標設定・進捗管理の徹底
- 理解中心の指導を徹底
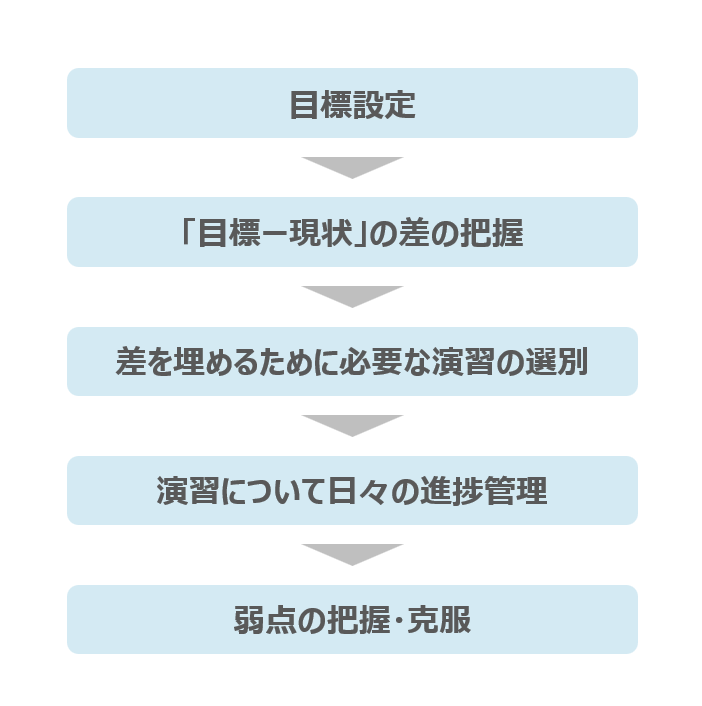

目標の設定・進捗管理の徹底では以下3つのステップで進めることで効率的に成績の向上に期待ができます。
- 目標の設定
- 必要な演習の選別
- 目標達成のための進捗の管理

それぞれご説明します。
私は指導前に必ず以下2つの目標を設定するようにしています。
- 最終的に達成したい目標
- 直近3か月で達成する目標
1つ目は大目標でみなさん1つ目はよく設定されていることが多いのです。一方で2つ目の中期目標については設定している方が少ない印象です。

当塾では 中期目標の達成を積み上げることで 、大目標の達成を目指します。
また、以下4点に意識しながら目標を設定しています。
- 具体的かどうか
- 測定可能かどうか
- 現実的かどうか
- 時間的制約があるかどうか
この4つを満たすことで 今必要な 対応策がグッと見えやすくなり、結果当塾の実績に繋がっていると自負しています。
4つのうちいずれかが欠けた場合どのような目標になるのかを例で見てみましょう。
3か月後までに成績アップ
現在偏差値50だが、3か月後までに偏差値70まで伸ばす
校内テストで80点を超える
いずれも掲げている目標はすばらしいのですが、今一つパッとしません。当塾は目標は達成するために設定するのであって、いつか叶えばよいという希望的観測のもとに設定するものではないと考えています。
そのため、上記の目標は例えば次のように書き換わります。
現在高校1年生で偏差値50だが、入試までに偏差値70まで伸ばしたい。そのためにまずは3か月後の校内テストで各科目前回+10点、つまり平均70点を目指す。

こう書くと将来像とそのために今やるべきことがはっきりしますね。
では、「3か月後の校内テストで各科目前回+10点、つまり平均70点を目指す」ために具体的に何をするのか?生徒の代わりに このレールを引くのが当塾の役割 になり、次の「必要な演習の選別」に繋がります。
「計画的に勉強しましょう。」
おそらく1度はどこかで聞いたことがある言葉だと思います。ただ、実際にやってみると想像以上に難しいことがわかると思います。
実際に通っている塾の生徒でも
勉強のペースがわからない・・・
と悩んでいる方も多く、当塾は本人の代わりに勉強のペースの管理・進捗管理を行います。 必要な演習を必要なタイミングで提供するので、本人は問題の取り組みに専念することができます 。
当塾の進捗管理では以下2つの観点で管理しています。
- 正解率
- 理解率
正解率はその名の通り、問題を解いて答えがあったものの割合です。
理解率はなぜこの答えになるのか説明できる割合です。

当塾は 理解率を高めるために 演習を進めていきます
当塾のこれまでのデータを見ると、 理解率≒実際の成績であり、これは理解すれば忘れない ということの裏付けになると考えています。
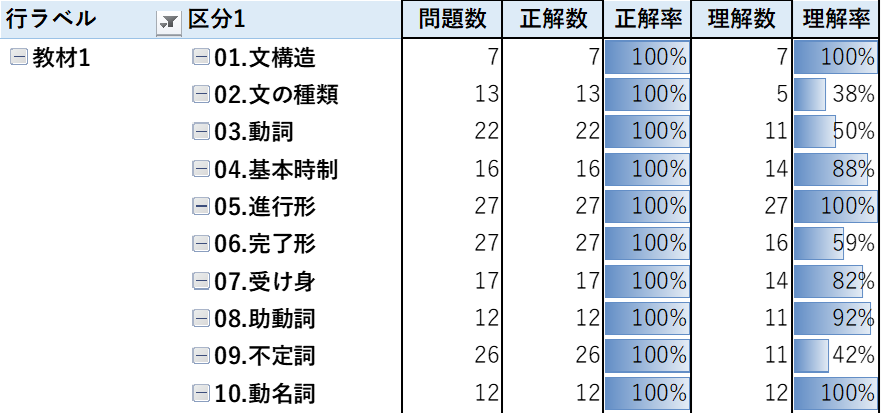
図は英語を指導している生徒の実際の進捗率の一例です。
これを見ると 日々の進捗を管理し 、演習を繰り返すことで正解率はいずれも100%になりました。一方で理解率を見ると「文構造」「進行形」「動名詞」は完璧である一方、 「文の種類」「不定詞」などの理解が足りない、つまり苦手分野である ことが確認できます。
したがって今後は苦手分野のみの演習で十分と言えます。

このようにどの分野を演習 しなくてよいか を明確にし、効率的に演習を進めていくことが学
力向上に繋がっていると自負しています。
このように 本人でも気づきにくい弱点をデータを用いて明らかにし 、「必要な演習の選別」が可能になります。この結果、効率的に弱点の克服が可能になり、成績が向上します。
最後に 効率的に成績を伸ばすために、弱点かつ本人のレベルに合わせた演習問題の選別を行い ます。
算数が苦手なので、九九を勉強します。
こう言われると「ちょっと待って」となるのではないでしょうか?
九九を勉強することで算数ができるようになり、苦手意識がなくなるのでしょうか?
たまたま九九だけが苦手な人はそれでいいですが、面積、濃度、簡単な方程式など算数と言えど範囲は広いです。なので自分に合った問題に取り組む必要があります。

そのために、当塾は今必要な分野・演習の選定を行います。
その結果、 効率的に苦手分野の克服・成績の向上が期待 できます。
また、当塾は理解しているかどうか、言い換えると 自分の言葉で説明できるかどうか を重要視しています。

当塾がなぜ理解を重要視するかを以下でご説明します。
結論から言うと、 理解中心の指導により応用力がつくため です。
ちょっと私の昔話に付き合っていただくと、私はもともと数学ができたわけではありません。むしろ反対に苦手意識すらありました。
当時通っていた塾の先生から「 暗記中心の学習から理解中心の学習に切り替えた方が絶対にいいよ 」と口酸っぱく言われていましたが、当時の私はそれを聞かず、公式を暗記し、ひたすら演習をこなすという勉強法を続けていました。

公式の証明を理解してもその問題出ないじゃん

1個1個理解してたら時間もかかるし、時間が足りないじゃん。
こうしたことを思いながら勉強した結果、高校2年生のときに校内試験で赤点(28点)を取ってしまいました。

さすがに焦った私は塾の先生に

なぜ理解して学ぶことが重要なのでしょうか?
と聞いたところ、その理由に納得できたので、その日から勉強法を改めました。その結果、 赤点を取ってしまうような私でしたが、最終的には全国模試で1位を取るまで数学の成績を上げる ことができました。
また高校を卒業して10年以上経った今でも、勉強せずに数検準1級に合格できたのは当時の理解中心の学習をしていたからです。
この経験から皆さんにお伝えしたいことは2つです。
- 理解中心で勉強すると応用力、つまり受験問題を解ききるために十分な力が付く
- 理解中心で勉強したことは忘れないため、結果として復習の回数が少なく済み、何度も暗記するより効率的
物事を理解するまでには、どうしても時間がかかります。そのため 当塾の指導法が最短で成績を伸ばす方法とは思っていません 。
ただ、 長期的に見て着実に成績を伸ばす方法である ことは、自信を持ってYesと言えます。
ここまで読んでいただきありがとうございます。成績が上がること以外で当塾で学ぶ上でのメリットをいくつか紹介いたします。
- 受験のテクニックについて指導
- 日々の学習を少しでも改善する方法
以下4点についても指導しています。
- 加点されやすい解答の作り方
- 減点されやすい解答の例
- 当日の心構え、準備するもの
- 試験・模試の受け方
特に1.と2.はおまけとは言えないほど重要です。
同じ内容を解答していても 10点満点で10点となる解答 と10点満点で7点になる解答が存在します.
何が減点されるのか?あるいは加点されるのか?
こうしたことを生徒は日々学んでいます。
以下4点についても指導しています。
- ノートの取り方
- 予習のやり方
- 復習のやり方
生徒は講義だけでなく、家や学校の学習でも理解を進めるよう指導しています。
例えばノートの取り方について一例を紹介します。
まず大切なことは、 自分にとって見やすいノートを作ること です。極論を言えば見直す自分が見やすければ第三者が見て見づらくでも問題ありません。
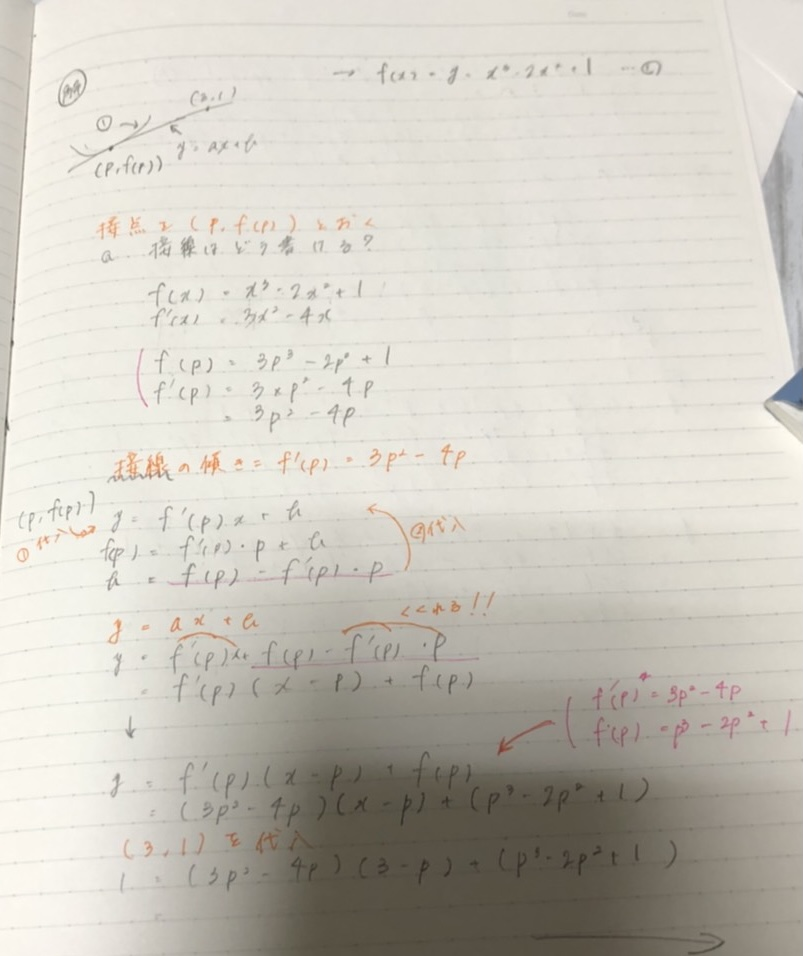
この生徒は指導後に以下のことを気を付けてノートを取るようになりました。
- 後で書き込みができるよう余白は多めに
- 関連する算式は赤で書く
- 不明点はオレンジで書く
こうすることで 見直す範囲がオレンジ・赤に絞れ、効率的に復習できた。黒の部分を見直さなくていいという気持ち的な余裕ができて復習の意欲が出た とお話しています。
数字で見る大学受験の現実
以下4つを数字の観点から見ていきましょう.
- 学年別平均勉強時間
- 第一志望の合格率
- 現役と浪人の比率
- 通塾率
※全てのデータに言えますが、一概にはこれが正しいとは言えません。あくまで、全国規模で見たときの平均となります。
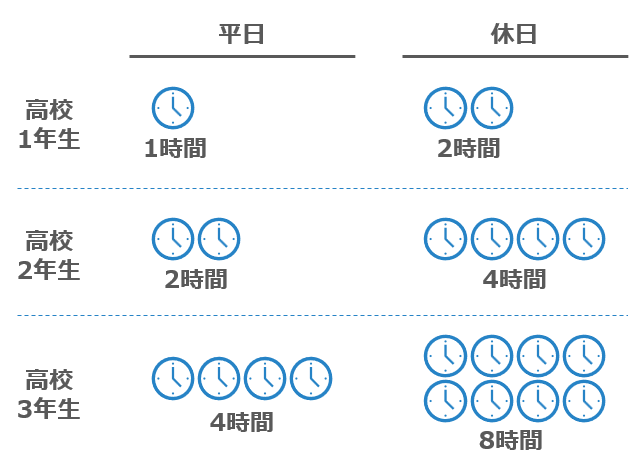
平日も休日も学年を追うごとに勉強時間は増えていきます。学校で忙しい平日とは異なり、休日は伸び率が大きいと言えます。言い換えると、どれだけ時間をとれるかは大きく個人差が出ることになります。

1,2年生の方は今から毎日15分でも長く取り組むように心がけましょう。後々良かったと感じるときが来ると思います。
1日15分と言えど、1年積み上げると90時間以上になります。
一説によると、ある科目の偏差値を1上げるのに必要な勉強時間は15~30時間だそうです。仮に30時間と仮定すると、1日15分多く続けることで1年で3も偏差値が変わります。

偏差値が3も変われば、志望校のレベルも1段階上がりますね。

驚いた方もいるのではないでしょうか。ただ、やはりこのくらいの数字が現実です。
理由について少し解説しますと、あなたの本当のライバルは誰でしょうか?
同じ大学を第一志望とする人
ではなく
その大学を滑り止めとして受ける人です。
(=学力的に1ランク上の人)
そうすると、どうしても第一志望の合格率は10%~20%前後になってしまうのです。
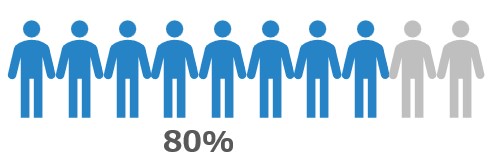
浪人生は5人に1人と言われています。
会場の多くは現役生なので、気負いせずに全力を出し切りましょう!
ちなみに、難関大ほど現役生は少なくなり、浪人生の数は増えるようです。
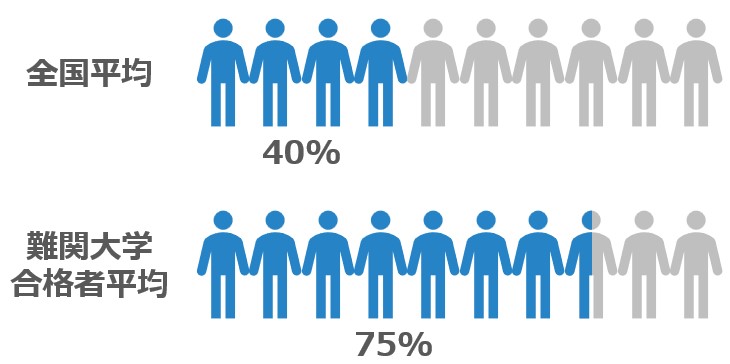
これを見るとやはり難関大合格にはまだまだ塾は必要なようです。
理由としては以下3つが大きいと言えます。
- 学校では必要な範囲をカバーできない
- 大学ごとの対策が学校の指導上難しい
- 難関大学ほど浪人生が増え、浪人生の多くは予備校で対策しているため
※全てのデータに言えますが、一概にはこれが正しいとは言えません。あくまで、全国規模で見たときの平均となります。
いかがでしたでしょうか。
知らない一面もあったかと思います。
ぜひ、こうした情報も入れながら、勉強していければと思っています。
料金


例えば、1回2時間の指導・徒歩圏内・ご自宅での指導の場合、月額28,000円になります。( = 3,500×2×4)
お問い合わせについて、スマホはページ最下部・PCはサイドバーから必要事項を記入の上、お気軽にご相談ください!
コラム:数学と算数の違い・そして苦手な人が多い理由
ここまで読んでいただきありがとうございます。
最後に私からのささやかなプレゼントとして
- 算数と数学の違い
- 数学を苦手とする生徒が多い理由
この2つについて、僭越ながら私なりの解釈と その解決策の1つをお伝えしたい と思います。少しでも苦手の克服・成績の向上に役立てば幸いです。
結論から言うと、算数と数学の違いは 学問を通して測る能力が変わる ということです。
算数はその名の通り「数を計算する」学問ですので、 算数は計算の速度や正確性を測る学問 と言えます。
例えば次のような問題が出た場合、

誰がどう計算しても答えは4分の5倍になります。

大事なことは4分の5倍が出せたかどうかであって、どう出したかはそこまで重要ではありません。
一方で数学はその名の通り「数を学ぶ」学問ですので、 どう答えまで到達したかその過程を測る学問 言えます。
そのため、答えだけ書いて、それが合っていたとしても満点をもらえないことも多々あります。
私はよく山登りを用いて説明しますが、算数は山の頂点に何があるかがわかればOK、数学はどうやって山の頂点に上るか・上った先に何があるかが重要とお伝えしています。

なので、数学では同じ満点でも解答が異なることはよくあります。それは同じ山の頂上には着いたけどルートが異なったケースと同じです。
繰り返しになりますが、算数と数学は 学問を通して測る能力が変わる 点が異なる、ここを抑えておきましょう。
結論から言うと、 算数と同じ方法で数学を勉強してしまうため です。
先ほどの話に繋がりますが、算数と数学では測る能力が変わります。
測る能力が変わるということは、 算数と数学は異なる方法・観点での勉強が必要 ということになります。
- 公式を覚えているか?
- わからない場合、答えをすぐに見て納得する
もしあなたがこうした観点で勉強をしているのであれば、少なからず数学に苦手意識があるのではないでしょうか。
例えば公式を覚えているかどうかは山登りでいえば道具を揃えたかどうかです。

道具を揃えたからといって、山を登れるわけではありません。道具の使い方や使う局面を理解して初めて道具は活きます。
次にわからない場合、答えをすぐに見て納得するのは山登りでいえば、他人が頂上に到達したのを見て満足した状態に近いです。

他人の登頂を見たからといって、自分が山を登れるわけではありません。体力や細かなルートを抑えてようやく登頂できるんです。
このように算数と数学は根本的に異なるため、数学に合わせた対応が必要になります。
1つ笑い話をしておくと、塾長の周りの数学者はそんなことはないですが、数学者同士でご飯を食べた際に割り勘の金額が出せないということはあるあるだそうです。
数学者=計算がめちゃくちゃできる=算数なんて楽勝 のように感じますが、決してそんなことはないということを証明するエピソードになります。
なぜこうしたことが起こるのか?と言えば、繰り返しになりますが、算数と数学は求められる能力が異なるためです。その数学者は数学に求められる能力は高いが算数に求められる能力は低かったということになります。

この話を通して伝えたかったことは、そのくらい算数と数学は別の科目ということです。
お待たせしました。そうした悩みを持つあなたに1つの解決策をお伝えします。
それは 1つの問題に3回なぜ?と問い、それに解答すること です。
それだけ?と思ったかもしれませんが、本当にそれだけです。
- なぜその公式を使うのか?
- なぜ解答の出だしがそうなるのか?
- なぜこの解き方ではダメなのか?
こうしたことを問題ごとに考えて「あぁ、だからそうなるのか」と納得して進めることができれば、半年後には数学の成績は上がっていることと思います。
もしあなたがこの方法に疑問を抱いているのであれば、それは算数に合わせた勉強方法で物事を考えているからかもしれません。

むしろ 今のその思考・勉強法の積み重ねの結果が今の成績に繋がっている わけです。
であれば、成績が取れていれば問題ありませんが、そうでないのであれば半年とは言いませんが3か月騙されたと思って取り組む価値はある勉強法だと思います。
ぜひあなたの数学の成績が伸びることを祈っております。
また、 当塾の指導ではこの方法も含む3つの勉強法を併用することで、より効率的に成績向上を目指すことができます 。その実績は先に見ていただいた通りですが、同規模の塾で当塾と同じくらい有名大学への合格割合が高い塾はあまり聞いたことがありません。
お問い合わせについて、スマホはページ最下部・PCはサイドバーから必要事項を記入の上、お気軽にご相談ください!